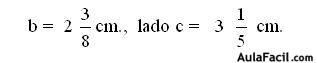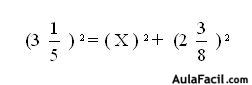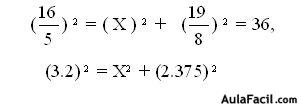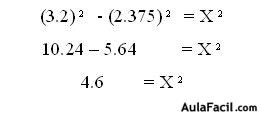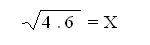CRITERIOS DE SEMEJANZAS ENTRE TRIÁNGULOS - DEFINICIÓN Y EJEMPLO

Criterios de semejanzas entre triángulos

     Debido a las propiedades de todo triángulo, las condiciones de semejanza impuestas pueden ser reducidas al estudio de los siguientes criterios de semejanza.

    Llamaremos criterio de semejanzas de dos triángulos a un conjunto de condiciones tales que, si se cumple, tendremos la seguridad que los triángulo son semejantes.

Primer criterio de semejanza o criterio LAL (Lado-Angulo-Lado)

    Si un triángulo es congruente a un ángulo β de otro triángulo y las medidas de los lados que forman el ángulo son proporcionales a las medidas de los lados que forman el ángulo β, entonces dichos triángulo son semejantes.

Ejemplo:
                  1. 

       
 
 
 

    Son semejantes porque tienen los lados proporcionales.

Segundo criterio de semejanza o criterio AA (Ángulo-Ángulo)

    Si dos ángulos de un triángulo son congruentes a dos ángulos de otro triángulo, entonces ambos triángulo son semejantes.

Ejemplo:

1. 

180º − 100º − 60º = 20º

   Son semejantes porque tienen dos ángulos iguales.

Tercer criterio de semejanza o criterio LLL (Lado-Lado-Lado)

    Son las medidas de los lados de un triángulo son proporcionales a las medidas de los lados de otro triángulo, entonces ambos triángulos son semejantes.

Ejemplo:

1. 

    Son semejantes porque tienen dos lados proporcionales y un ángulo igual.

SEMEJANZAS DE FIGURAS PLANAS - DEFINICIÓN Y EJEMPLO

Semejanzas de Figuras Planas

 
    Dos figuras son semejantes si tienen la misma forma aunque no tengan el mismo tamaño.

    Dos polígonos son semejantes si existe una correspondencia biunívoca entre sus vértices tal que sus ángulos correspondientes son congruentes y sus lados correspondientes son proporcionales. Esta semejanza se denota con el símbolo ~.



Ejemplos:





1.

2.

TEOREMA DE TALES Y APLICACIONES - DEFINICIÓN Y EJEMPLO

Teorema de Tales 

    El teorema de Tales establece los siguientes enunciados:

• Los segmentos determinados son rectas paralelas sobre dos rectas secantes cualesquiera son proporcionales.
• Si son varias rectas cortadas por dos transversales los segmentos son proporcionales, entonces dichas rectas son paralelas.

                                  

Aplicaciones del Teorema de Tales en los Triangulos

Dado un triángulo ABC, si se traza un segmento paralelo, B1 C1, a uno de los lados del triángulo , se obtiene otro triángulo AB1C1, cuyos lados son proporcionales a los del triángulo ABC.

     

Ejemplo:

1. Hallar las medidas de los segmentos a y b.

 

TEOREMA DE EUCLIDES Y APLICACIONES - DEFINICIÓN Y EJEMPLO

Teorema de Euclides

    En el triángulo ABC rectángulo en C se ha trazado la altura CD=h correspondiente a su hipotenusa, donde c=AB. Esa altura determina sobre la hipotenusa dos segmentos de medidas m y n que son las proyecciones ortogonales de los catetos de medidas b y a, respectivamente, sobre la hipotenusa. sobre este triángulo se anuncian dos proporciones del teorema de Euclides, conocidas como el teorema de la altura y el teorema del cateto.

Teorema de la altura

    En todo triángulo rectángulo se cumple que el cuadrado de la altura correspondiente a la hipotenusa es igual al producto de los segmentos que ella determina sobre la hipotenusa.

Ejemplo:

1. En la figura a la derecha, determinar h,

si p = 2 y q = 8

Teorema del cateto

      En todo triángulo rectángulo se cumple que el cuadrado de la medida de un cateto es el productos de la medida de la hipotenusa y de la medida de la proyección ortogonal del cateto sobre la hipotenusa.

Ejemplo:

1. La hipotenusa de una triángulo rectángulo mide 30 cm y la proyección de un cateto sobre ella 10.8 cm. hallar el otro cateto.

   

TEOREMA DE PITÁGORAS - DEFINICIÓN Y EJEMPLO

    Teorema de pitágoras

     El teorema de Pitágoras indica que un triángulo es rectángulo si y solo si el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las longitudes de sus catetos.

                                    a² + b² = c²

    La aplicación de este teorema permite resolver ejercicios que involucran triángulos rectángulos y las medidas de sus lados.

    Ejemplos:

1. Teniendo los catetos a=3 y b=4, tendríamos que la hipotenusa sería:

2.  Se tienen los lados de un Triángulo Rectángulo a = X cm. y 

Aplicamos la Fórmula:

1. Sustituimos los valores dados;

2. Resolvemos las fracciones mixtas:

3. Despejamos la Ecuación y resolvemos los cuadrados:

4. Pasamos el cuadrado al otro lado, convirtiéndolo en raíz cuadrada:

5. Obteniendo como respuesta 2.14 = X = a

NOTA: La Hipotenusa siempre debe ser mayor que los catetos. Si cualquiera de los catetos es mayor no es Equivalente, también no lo es si la Hipotenusa es igual a los catetos.

  

GEOMETRÍA DEL PLANO - DEFINICIÓN Y EJEMPLO

Geometría del plano 

    Geometría del plano, del griego geo, tierra, metrine, medir, rama de la matemática que se ocupa de las propiedades del espacio. En su forma mas elemental, la geometría se preocupa de problemas métricos como el cálculo del área y el cálculo de figuras planas y de analítica, geometría descriptiva, tropología, geometría del espacio, con cuatro o más dimensiones, geométrica fractal, geometría no euclidea.

    Su proposito es desarrollar el mensamiento abstracto a traves dele studio de las relaciones geometricas enmtre figuras planas y sus elemnetos. reconocer la utilidad de geometria para escribir y resolver situaciones cotidianas.

Plano

    Un plano es un objeto ideal que solo posee dos dimensiones, y contiene infinitos puntos y rectas; es un concepto fundamental de la geometría junto con el punto y la recta.

    Un plano queda definido por los siguientes elementos geométricas:

• Tres puntos no alineados.
• Una recta y un punto exterior a ella.
• Dos rectas paralelas o dos rectas que se cortan.

Geometría del plano en nuestra vida diaria 

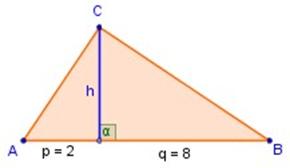
    El trabajo de carpintería requiere tener mucho conocimiento de geometría para poder construir muebles, closet, cocina y hasta casas. Para ello se usan por ejemplo, varios teoremas importantes, así como propiedades de semejanzas y congruencia entre figuras.

Carpintería: madera, serruchos...¿y teorema?

    Antes de  desarrollar un proyecto de construcción, como una casa de madera, es importante conocer los tamaños, las dimensiones y los ángulos. Algunos de estos se hallan usando teoremas matemáticos de geometría.

                           

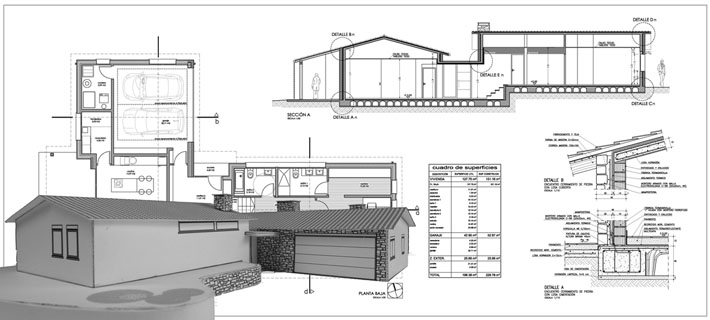
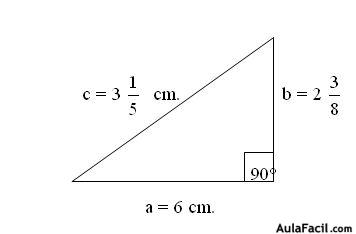
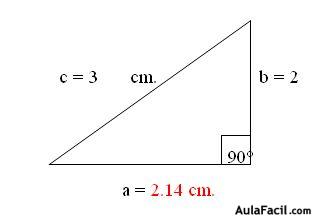
     Del diseño o dibujo de la casa, se pueden determinar ciertas medidas, usando solo geometría aplicada. Con el teorema de tales es posible hallar las medidas que tiene que tener las vigas del techo, pues estas deben mantener la proporción que establece este teorema. Por su parte, las medidas que tendrá la superficie del mismo se puede calcular a través del uso del teorema de pitagoras.