TEOREMA DE EUCLIDES Y APLICACIONES - DEFINICIÓN Y EJEMPLO

Teorema de Euclides

    En el triángulo ABC rectángulo en C se ha trazado la altura CD=h correspondiente a su hipotenusa, donde c=AB. Esa altura determina sobre la hipotenusa dos segmentos de medidas m y n que son las proyecciones ortogonales de los catetos de medidas b y a, respectivamente, sobre la hipotenusa. sobre este triángulo se anuncian dos proporciones del teorema de Euclides, conocidas como el teorema de la altura y el teorema del cateto.

Teorema de la altura

    En todo triángulo rectángulo se cumple que el cuadrado de la altura correspondiente a la hipotenusa es igual al producto de los segmentos que ella determina sobre la hipotenusa.

Ejemplo:

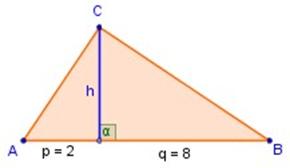
1. En la figura a la derecha, determinar h,

si p = 2 y q = 8

Teorema del cateto

      En todo triángulo rectángulo se cumple que el cuadrado de la medida de un cateto es el productos de la medida de la hipotenusa y de la medida de la proyección ortogonal del cateto sobre la hipotenusa.

Ejemplo:

1. La hipotenusa de una triángulo rectángulo mide 30 cm y la proyección de un cateto sobre ella 10.8 cm. hallar el otro cateto.